Chapter 5 Interior Point Methods
Inequality constrained minimization problems can be written as
\[\begin{align} \tag{5.1} \text{minimize}& & f_0(x) & & \\ \text{subject to}& & f_i(x) \leq 0, & & i = 1,\dots,m \\ & & Ax=b & \end{align}\]
where \(f_0,\dots,f_m:\mathbf{R}^n\rightarrow \mathbf R^n\) are convex and \(\mathcal{C}^2\) differentiable, and \(A\in \mathbf R^{p\times n}\) with \(\mathbf{rank} A = p < n\) (Boyd and Vandenberghe 2004). Assuming that the solution \(x^*\) exists with the optimum value \(p^* = f_0(x^*)\).
5.1 KKT conditions
\[\begin{align} \tag{5.2} Ax^* = b, f_i(x^*) & \leq & 0 &, & i=1,\dots, m \\ \lambda^* & \leq & 0 & & \\ \nabla f_0(x^*) + \sum_{i=1}^{m} \lambda^*_i \nabla f_i(x^*) + A^Tv^* & = & 0 & & \\ \lambda^*_i f_i(x^*) & = & 0 &, & i=1,\dots,m \end{align}\]
The KKT conditions (5.2) means, respectively:
- All constraints are satisified at \(x^*\);
- Corresponding Lagrange multiplier is sufficiently larger than zero;
- The gradient of the Lagrangian at \(x^*\) is 0;
- Inequality constraints are either inactive or on the edge.
5.2 Logarithmic barrier function and central path
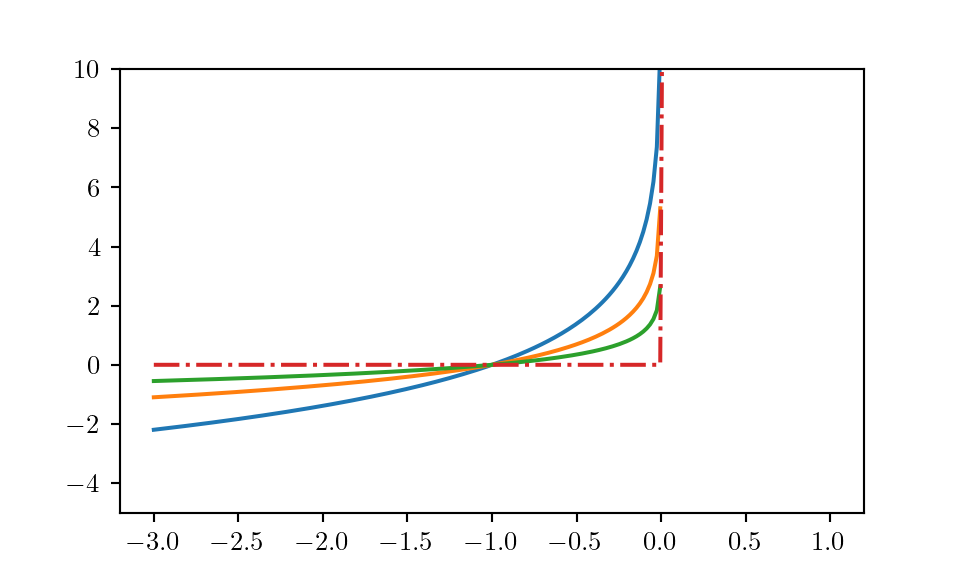
The aim is to approximate (5.1) as an equality-constrained problem and apply Newton’s method. This proposes the following formulation: \[\begin{align} \tag{5.3} \text{minimize}& & f_0(x) + \sum_{i=1}^m I_{-}(f_i(x)) \\ \text{subject to}& & Ax = b, \end{align}\] where \(I_{-} : \mathrm R \rightarrow \mathrm R\) is the indicator function \[\begin{equation} \tag{5.4} I_{-}(u) = \begin{cases} 0 & u\leq 0 \\ \infty & u > 0. \end{cases} \end{equation}\]
However, it is obvious that (5.3) is non-differentiable, so we cannot optimize it with Newton’s method.